במסלול אליפטי סביב טיכו וקפלר
מבוא:
עבורנו השמיים תמיד היו במידה מסוימת סתומים. והעובדה הזו, שלא צריך מכשור מתקדם במיוחד על מנת להפיק מדידות איכותיות ולהפיק מהן ידע בעל ערך תמיד הייתה עבורנו כמעין אתגר והזמנה.
השנה הזו בה מתאפשר לנו לחקור תופעה בעצמנו ונותנים לנו את הזמן והמשאבים לכך הייתה הזדמנות פז להיענות לאתגר ולהתחיל לפענח את סודות השמיים.
מטרות המחקר ושאלות המחקר:
מטרת המחקר היא להתחקות אחר התהליך המדעי שעבר קפלר, באמצעות קודמיו. אנו נרצה להראות שהמודל האליפטי הוא המודל הטוב ביותר לתאר את מסלול כוכבי הלכת סביב השמש. מושאי המחקר הם מסלולי כדור הארץ ומאדים סביב השמש, בהתבסס על מדידות טיכו.
- כיצד ניתן בעזרת הסתכלות בשמיים ועריכת מדידות "בעין בלתי מזוינת", להסיק את תנועתיהם של כוכבי הלכת סביב השמש?
- איך להגיע לאיכות המדידה של טיכו ברהה באמצעות מכשירי מדידה אנלוגיים? על פי מקורות שונים, רמת הדיוק שלו היתה בין 5 ל300 שניות מעלה (שנית מעלה = 1/3600 מעלה)
- מהם הפרמטרים המתארים בצורה המדויקת ביותר את תנועת מאדים וכדור הארץ סביב השמש? הפרמטרים שנרצה למצוא: אקסצנטריות ופֵּרִיהֶלְיוֹן של כדה"א ומאדים.
עקרונות פיזיקליים מרכזיים
שחזור עקרונות היסטוריים של קפלר וטיכו, מדידות זוויות של כוכבי לכת, הוכחת חוקי קפלר, חוק קפלר הראשון – כוכבי הלכת נעים במסלול אליפטי סביב השמש הנמצאת באחד ממוקדי האליפסה, מכשיר מדידה נוניוס
ניסויים מקדימים:
- מדידות כוכבי לכת – מדידת זוית נטיה באמצעות מד זוית "משודרג"
- מדידות כוכבי לכת – הפרש אלונגציה בין שני כוכבי לכת באמצעות מטה יעקב
- בניית מכשיר מדידה מדויק

ניסוי מרכזי:
- בדיקת מדידות טיכו מול תאוריה של מסלולים מעגליים ומהירות זויתית קבועה
- בדיקת מדידות טיכו מול תאוריה של מסלולים מעגליים כשהשמש לא במרכז
- בדיקת מדידות טיכו מול תאוריה של מסלולים אליפטיים
מהלך המחקר
המחקר שלנו התחלק לשני חלקים עיקריים:
בחלק הראשון נעשה מדידות וננסה להגיע לדיוק של טיכו באמצעות בניית מכשיר דומה.
החלק השני יתבסס על המדידות של טיכו (שהורדנו מהאינטרנט ומבוססים על הספר שלו), וננסה לשחזר את המסלול המחשבתי שקפלר עבר ונעבור דרך אבני הציון הבאות:
- ננסה לשלול את מודל המסלולים המעגליים של קופרניקוס שהשמש במרכזו במהירות זויתית שווה
- נעבור דרך מודל הביניים של קפלר, שהניח שהמסלול מעגלי, אך השמש לא במרכז המעגל, ומהירות זוויתית לא שווה
- המודל האליפטי בו השמש נמצאת באחד המוקדים והמהירות הזווית נקבעת לפי חוק השטחים השווים
ממצאים:
בחלק הראשון של המחקר בנינו מכשיר מדידה מדויק למדידת זויות כוכבים. לא הספקנו לערוך ניסוי מסכם באמצעות המכשיר שבנינו.


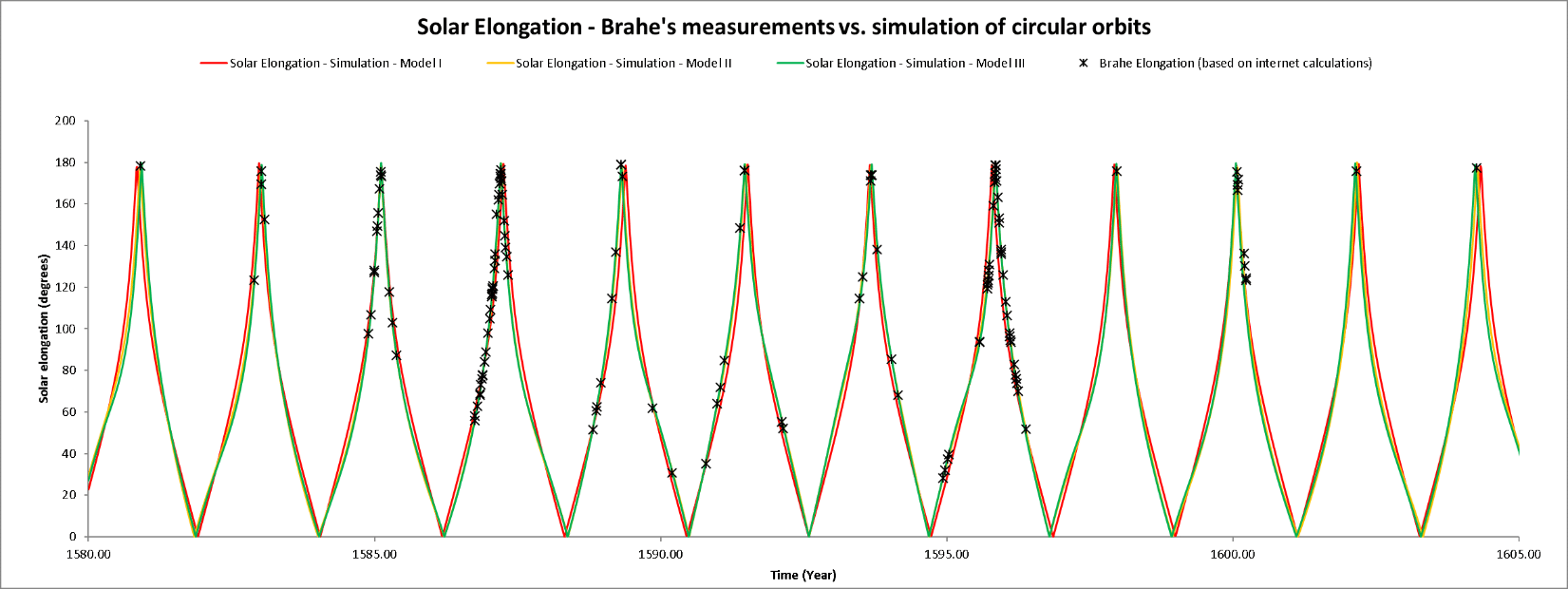
בחלק השני השווינו שלושה מודלים שונים מול המדידות של טיכו ברהה על כוכב הלכת מאדים.
מודל I – מסלול מעגלי כאשר השמש במרכז, ומהירות זויתית שווה
מודל II – מסלול מעגלי, כאשר השמש מוסטת מהמרכז, והתנועה היא לא שוות מהירות
מודל III – מסלול אליפטי, כשהשמש באחד המוקדים, והתנועה מכסה שטחים שווים בזמן שווה
| Mean Error [deg] | Max Error [deg] | R2 | |
| Model I | 16.53311819 | 32.00144868 | 0.913044 |
| Model II | 1.830621479 | 13.22812825 | 0.992983 |
| Model III | 3.54296465 | 17.39715694 | 0.984626 |
דיון ומסקנות:
לפי המחקר שלנו, בשלושת המדדים שבחרנו, המודל של מסלולים מעגליים עם שמש מוסטת הוא יותר מדויק מאשר מסלולים אליפטיים!
יש לכך סיבות רבות. ראשית, בשל השגיאה שמצאנו בהמרה מזוית ה-declination ל-solar elongation , איבדנו למעשה את רמת הדיוק של טיכו ברהה במדידות שלו. אנחנו משערים שקפלר ידע לעשות את ההמרה הזאת בצורה יותר מדויקת, וגם הוא השתמש בעיקר במדידות של ה-opposition ולאו דווקא בכל המדידות האחרות של טיכו. שנית, מצאנו שגיאות גם במדידות של טיכו (אמנם שגיאת סימן, ולא ברור אם השגיאה היא במקור או באקסל שמצאנו באינטרנט). שלישית, ראינו כי ה-solver זקוק לעזרה משמעותית כדי לקבל פתרונות אופטימליים, והיוריסטיקה שלו הרבה פעמים מוצאת פתרונות מקומיים. כמו כן, בגלל חוסר זמן, לא הספקנו להיכנס לעומק לדרך המחשבה של קפלר ואיך הוא התמודד עם המסלולים האליפטיים.
ביבליוגרפיה:
- Baden, D. (2019). Forces and Motion. Retrieved from University of Maryland – Department of Physics: https://www.physics.umd.edu/hep/drew/forces/#fig1
- Brahe, T. (1598). Astronomiæ instauratæ Mechanica – English translation – Small Quadrant of Gilt Brass. Retrieved from The Royal Library – National Library of Denmark and Copenhagen University Library: http://www5.kb.dk/en/nb/tema/webudstillinger/brahe_mechanica/brahe_fsi.html?page=12
- Brahe, T. (1602). Astronomiæ instauratæ mechanica. apud L. Hvlsivm.
- Christiana Honsberg, S. B. (2019). Declination Angle. Retrieved from PV Education.ORG: https://www.pveducation.org/pvcdrom/properties-of-sunlight/declination-angle
- Christianson, J. R. (2017). Tycho Brahe's Earliest Instruments. Retrieved from Nordic Journal of Renaissance Studies: https://www.njrs.dk/12_2017/12_christianson_brahe.pdf
- Cross, D. (n.d.). Solar System Calculator. Retrieved from Cosine Kitty: http://cosinekitty.com/solar_system.html
- Eremenko, A. (2016, Dec 17). How Kepler discovered his laws. Retrieved from Perdue Science: https://www.math.purdue.edu/~eremenko/dvi/kepler.pdf
- HAO. (2020). TYCHO BRAHE'S OBSERVATIONS AND INSTRUMENTS. Retrieved from HAO High Altitude Observatory: https://www2.hao.ucar.edu/Education/FamousSolarPhysicists/tycho-brahes-observations-instruments
- Hwang, J. (n.d.). Kepler and the First Law of Planetary Motion. Retrieved from Mathematics + Berkeley: https://math.berkeley.edu/~robin/Kepler/index.html
- Iron sights. (n.d.). Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Iron_sights
- Johannes Kepler's New Astronomy. (2006). Retrieved from Larouche PAC: https://science.larouchepac.com/kepler/newastronomy/newastronomy.html
- Nonius (device). (2020). Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Nonius_(device)
- Pafko, W. (2000). Visualizing Tycho Brahe's Mars Data. Retrieved from Visualizing Tycho Brahe's Mars Observations: http://www.pafko.com/tycho/observe.html
- Poelje, O. v. (2004). Diagonals and Transversals: Magnifying the Scale. Journal of the Oughtred Society, 22-28. Retrieved from https://eeuwen.home.xs4all.nl/images/Pics/Kombuispraat/Pleinschaal/200410%20Diagonals%20and%20Transversals%20V13-2.pdf
- Science, E. A. (2007). Twelve Observations of Mars. Retrieved from Kepler's Dicovery: https://www.keplersdiscovery.com/CorrectedTable.html
- Wesley, W. G. (1979). TYCHO Brahe's Solar Observations. Journal for the History of Astronomy, Vol. 10, 96-101.
- גירבין, ג. (2010). היסטוריה של המדע 1543-2001. ידיעות ספרים.
- סמבורסקי, ש. (1981). אישיותו המדעית של קפלר. מדע, 12-15.
- פורטר, נ. (2001). קפלר – בין דת לדעת. גלילאו, 65-68.
- קסלר, א. (1970). יוהאנס קפלר – האיש ופועלו, ביוגרפיה . דביר ועם עובד.


