אווירודינמיקה כנף מטוס
מבוא:
כאשר נפגשנו לראשונה על מנת לבצע את העבודה חשבנו ביחד רבות על איזה נושא אנו רוצים לחקור בעבודתנו, אחרי שבדקנו נושאים שונים הגענו למסקנה שאנו רוצים לחקור תנועת מטוס בשמיים. תנועת המטוס עניינה אותנו מאוד ולאחר בדיקה של איזה נושאים במטוס אנו יכולים לחקור החלטנו להתמקד בשאלה כיצד ניתן לבנות מטוס שיטוס בצורה היעילה ביותר. ולכן החלטנו לחקור את הכנפיים של המטוס , ובסוף המחקר נוכל לדעת מהי הכנף האידיאלית שאיתה הטיסה תהיה יעילה ביותר וכך תהיה חסכונית כלומר שתבזבז כמה שפחות דלק ואנרגיה. נושא זה עלה לראשנו בעקבות היותנו ספורטאים עופר בטניס ויואב בשייט, ובשייט יש הרבה קשר לכנף מטוס כי בעצם המפרש מייצר כוח להזיז את הסירה כמו כנף מטוס.
עקרונות פיזיקליים מרכזיים:
כוח עילוי , כוח גרר, זווית התקפה אופטימאלית של כנף שטוחה בזמן טיסה, עקרון ברנולי, חקירת יחס עילוי גרר כתלות ברדיוס העקמומיות.
מטרת המחקר:
– הבנה מעמיקה של כוחות העילוי והגרר ושל התופעות הפיזיקאליות הגורמות להיווצרותם.
– חקירת תנועת כנפי המטוס , והבנת הכוחות שהן מייצרות.
– למידת התופעות הפיזיקאליות המייצרות את הכוחות הפועלים על כנף מטוס בעת מעופו, כמו : זווית התקפה , עקרון ברנולי…
– הכרה נרחבת עם שיטות מחקר מתקדמות בתחום , כמו עבודה עם מנהרת רוח ובניית דגמים לצורך ניסויים ומחקר.
שאלות המחקר:
1) מציאת זווית התקפה אופטימאלית של כנף שטוחה בזמן טיסה.(1
2) חקירת יחס עילוי גרר כתלות ברדיוס העקמומיות.
מהלך המחקר :
העבודה כללה שני ניסויים ראשיים כדי לענות על שאלות המחקר לעיל.
הניסוי הראשי הראשון :
מיקדנו את המאוורר על מהירות קבועה של 3.5 מטר לשנייה, לאחר מכן מדדנו את זווית ההתקפה של הכנף בעסזרת מד זווית ושינינו את הזווית לפי הצורך בקפיצות של 5 מעלות. כל פעם מדדנו את הכוחות העילוי והגרר בעזרת חיישני כוח המחוברים לתוכנת multilub .
באיור 1 מתאורת מערכת הניסוי)

איור 1
הניסוי הראשי השני :
בינינו כנפיים עבור רדיוסים שונים והכנסנו אותם למנהרת הרוח (ראו איור 1 -מערכת ניסוי ) ומדדנו את כוח העילוי והגרר על ידי חיישני כוח המחוברים לתוכנת הmultilub .ושרטטנו שלושה גרפים של כוח הגרר כתלות ברדיוס העקמומיות.


(איור 1 )
ממצאים:
הניסוי הראשי הראשון :
שרטטנו גרף יחס עילוי גרר כתלות בזווית ההתקפה ואת ההשוואה לתאוריה עשינו באמצעות שיטת solver בExel:
ניתן לראות מהגרף הנ"ל יצא כי הזווית המקבלת את יחס העילוי\גרר הגבוה ולכן היא גם החסכונית ביותר מן כל הזוויות שבדקנו היא בערך 8 מעלות.
הניסוי הראשי השני :
בסוף הניסוי שרטטנו גרף יחס עילוי גרר כתלות ברדיוס העקמומיות אבל ,לא יכולנו להסיק מגרף זה מסקנות מכיוון שיצאו תוצאות לא ברורות ולדעתנו הסיבה לכך שככל שרדיוסי העקמומיות גדלים כך כל שגיאה קטנה תשפיע על התוצאות (על היחס עילוי גרר).
דיון ומסקנות:
הניסוי הראשי הראשון :
מהגרף הנ"ל יצא כי הזווית המקבלת את יחס העילוי\גרר הגבוה ולכן היא גם החסכונית ביותר מן כל הזוויות שבדקנו היא בערך 8 מעלות, את ההשוואה לתאוריה עשינו באמצעות שיטת solver באקסל.
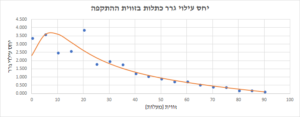
ניתן לראות מהגרף שבזוויות נמוכות ( מעלות 0-20) הגרף מאוד מפוזר , ואחר כך הנקודות מתאימות יותר . זה בגלל שהמקדמים קטנים משמעותית בזוויות הקטנות להבדל מזוויות גדולות ולכן כל שינוי קטן במקדמים משנה דרמטית את היחס ביניהם
הניסוי הראשי השני :
מטרת הניסוי הייתה למצוא קשר בין עקמומיות הכנף לבין כוח העילוי וכוח הגרר על מנת למצוא רדיוס עקמומיות אופטימאלי לכנף שאיתה הטיסה תהיה יעילה ביותר וכך תהיה חסכונית כלומר תבזבז כמה שפחות דלק ואנרגיה. אבל עקב משבר הקורונה הצלחנו לעבוד יותר על הפיתוחים המתמטיים של הניסוי ופחות על התוצאות באופן מעשי. ולכן אני ממליצה להמשך המחקר לעבוד על הרכבת מערכת וכנפיים יותר מדויקות על מנת לקבל תוצאות יותר מותאמות ומדויקות לרקע התיאורטי שיאפשרו להגיע למסקנה לגבי הקשר בין עקמומיות הכנף ויחס עילוי/ גרר. בנוסף לכך, הייתי ממליצה בניסוי מדידת כוח העילוי כתלות ברדיוס שהכנף תהיה הפוכה במנהרת הרוח (שהצד הקמור כלפי מטה). ככה הכנף הייתה לוחצת על מד הכוח במקום לנסות להתרומם ממנו


