מבוא:

מטוטלת מתמטית היא משקולת תלויה על חוט, כאשר המטוטלת נעה בזוויות קטנות נקרא לתנועה: תנועה הרמונית פשוטה.

אנחנו חוקרים את הנושא : מטוטלת מציירת. בחרנו בנושא זה אחרי שראינו סרטון ביוטיוב למטוטלת עם מיכל צבע שמציירת צורות שונות, מורכבות ויפות. אהבנו מאוד את הרעיון ורצינו ליישם ולבנות מטוטלת כמו בסרטון ולחקור את המשתנים המשפיעים על הצורות .

בהתחלה בדקנו מה משפיע על זמן המחזור ולאחר מכן התחלנו לחקור את מסלול התנועה של מטוטלת מהצורה Y.

הצורות שנוצרות מהמטוטלת המציירת נקראות צורות ליסאז'ו. במחקר שלנו נסינו לאפיין את התנועה ולהבין אותה לעומק.

מטרות המחקר ושאלות המחקר:

שאלות המחקר

• אילו פרמטרים משפיעים על תנועת מטוטלת מתמטית וכיצד הם משפיעים?
• איך נוצרות צורות ליסז'ו?
• כיצד אורכי החוטים ונקודת הקשר במטוטלת מסוג Y משפיעה על הצורות שנוצרות?
• אילו פרמטרים נוספים משפיעים על הצורות שנוצרות?

מטרות העבודה

• חקירת הגורמים המשפיעים על זמן מחזור של מטוטלת פשוטה .
• חקירת מסלול תנועתה של מטוטלת פשוטה .
• חקירת צורות ליסז'ו הנוצרות ממטוטלת בצורת Y.
• הכרה נרחבת עם שיטות מחקר מתקדמים בתחום, כמו עבודה עם Tracker ובניית דגמים לצורך ניסויים וחקר.

מהלך המחקר

1. בנינו את המערכת המשורטטת בתרשים הבא: 
2. 
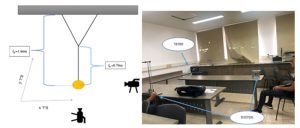
3. מיקמנו שתי מצלמות כך שכל מצלמה תתעד ציר אחד של התנועה
4. הפעלנו סטופר ברקע ודאגנו שיופיע במסך של שתי המצלמות בו זמנית.
5. שחררנו את הגוף מנקודה המרוחקת ב m3 מנקודת שיווי המשקל
6. צילמנו את התנועה
7. ניתחנו כל אחד מהסרטונים בתוכנת tracker, חתכנו את שני הסרטונים כך שיתחילו ויסיימו באתו רגע לפי הסטופר .
8. ערכנו טבלה באקסל של המיקום האופקי של הגוף בכל רגע.
9. ניתחנו את התנועה בכל ציר בנפרד.
10. בנינו גרף למיקום X-Y על מנת לקבל את צורת ליסז'ו.
11. השווינו את הצורה שהתקבלה מהניתוח המתמטי עם הצורה שהתקבלה בפועל.

ממצאים:

ציר X:

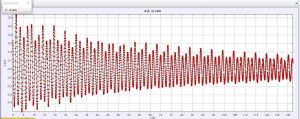
ציר Y:

 כפי שניתן לראות בגרפים שהתקבלו בכל ציר, המשרעת של התנועה אכן דועכת, (הולכת וקטנה עם הזמן בגלל החיכוך) . אך ניתן לראות תופעה "מוזרה" שלא ציפינו לה והיא שהמשרעת באופן מקומי  פעם גדלה ופעם אחרת קטנה וכך לסירוגין.

חשבנו בהתחלה שהשינוי במשרעת נובע מהיפוך אנרגיות בין הצירים, כלומר האנרגיה בציר X קטנה בגלל שהאנרגיה בציר Y גדלה וכך הלאה. בגלל כך, חישבנו את האנרגיה הכוללת בכל ציר, סכמנו אותם ושרטטנו גרף אנרגיה – זמן . קיבלנו אותן "הפרעות". לאחר מכן, הבנו שהבעיה נובעת מהניתוח של תוכנת טרקר בשל המרחק המשתנה מהמצלמה ובשל הגודל הלא נקודתי של הגוף.

 על מנת לחשב את מקדם הדעיכה של המשרעת הנובע מהחיכוך של המטוטלת עם האוויר, ערכנו באקסל טבלה עם הזמנים של התנועה כציר X ובציר Y את הערכים שמתקבלים מההצבה בביטוי:

x=e^(-t/b)∙A∙cos⁡(ω∙t+ϕ)

חישבנו את הערכים , ערכנו עמודה שבה חישבנו את ההפרש בריבוע בין הערך המחושב לפי התיאוריה והערך מהניסוי. סכמנו את הערכים והפעלנו את פונקציית ה solver באקסל על מנת להתאים את הפונקציה לנתונים ככל האפשר.

בציר הX קיבלנו:

b=61.2sec

בציר ה-Y קיבלנו:

b=221.81 sec

ניתן לראות מהתוצאות כי מקדם הדעיכה (b) גדול יותר בציר Y מאשר בציר X ועל כך הדעיכה הייתה איטית יותר בציר Y.

לפי הערכתנו עבודת החיכוך גדולה יותר בתנועה של החלק התחתון של המטוטלת בגלל הקשר בחוט. ששם ישנו החיכוך הגדול ביותר .

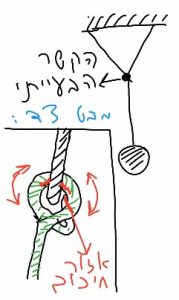
דיון ומסקנות:

מהניתוח של הסרטונים קיבלנו תנועה הרמונית פשוטה בכל ציר כך שהמשרעת קטנה עם הזמן בגלל החיכוך.

חישבנו את זמן המחזור התיאורטי  בכל ציר והשווינו עם זמן המחזור מהניסוי.

לאחר מכן ערכנו גרף X-Y של התנועה וקיבלנו:

 צורה זאת היא צורה ממשפחת צורות שנקראות צורות ליסז'ו..

בשלב שאחרי חישבנו את מקדם הדעיכה בכל ציר בדרך הבאה:

ערכנו באקסל טבלה עם הזמנים של התנועה כציר X ובציר Y את הערכים שמתקבלים מההצבה בביטוי:

x=e^(-t/b)∙A∙cos⁡(ω∙t+ϕ)

כאשר :

B – קבוע הדעיכה

A – משרעת התנועה

ω – התדירות הזוויתית

ϕ – זווית המופע

השתמשנו בפונקציית ה solver באקסל וכך חישבנו את מקדם הדעיכה בכל ציר (b). קיבלנו מקדמי דעיכה שונים בכל ציר, מקדם הדעיכה גדול יותר בציר Y מאשר בציר X ועל כך הדעיכה הייתה איטית יותר בציר Y.

לפי הערכתנו עבודת החיכוך גדולה יותר בתנועה של החלק התחתון של המטוטלת בגלל הקשר בחוט. ששם ישנו החיכוך הגדול ביותר .

כאמור, צורות אלו נקראות צורות ליסז'ו נוצרות כתוצאה מתנועה המורכבת מתנועה הרמונית פשוטה בשני צירים עם הפרש מופע ותדירות זוויתית.

השוני בתדירות הזוויתית נוצר כתוצאה ממבנה המטוטלת Y כך שהיא מאפשרת תנועה בשני הצירים, כאשר בכל ציר אורך החוט שונה ובכך גם התדירות וזמן המחזור.

בניסוי הצלחנו לבנות מודל לצורה ולהגיע לצורת ליסז'ו בדרך מתמטית על ידי ניתוח התנועה בכל ציר בנפרד.

בציר 1:       x1=e^(-t/b1)∙A∙cos (ω∙t+ϕ1)

בציר 2:    x2=e^(-t/b2)∙A∙cos (ω2∙t+ϕ2)  

בקובץ אקסל ניתן לערוך טבלה עם הפרשי זמן קבועים , לחשב את  בהתאם לערכים שנרצה לגבי אמפליטודה, תדירות ומשרעת. לחשב גם כן את  בציר השני ולבנות גרף  כפונקציה של . כך נקבל את צורת ליסז'ו שמתקבלת ממטוטלת מציירת מהצורה Y .

בניסוי שמתואר לעיל התמקדנו בגוף עם מסה קבועה . אך אילו היה לנו מספיק זמן תכננו לחקור האם השינוי במסה תוך כדי תנועה (כאשר הכלי מאבד מהמסה שלו כי החול נופל) האם שינוי זה משפיע על תדירות התנועה .

נכון שבאחד הניסויים המקדימים הוכחנו שהמסה לא משפיעה על התדירות אך אנו חושבים שעדיין יש מקום לחקור את הבעיה בגלל שהגוף מאבד מסה תוך כדי תנועה וזה גורם לשינוי בתנע שלו מה שיכול להשפיע על הצורות או התדירות.