מבוא:

 בעבודה זו, נעסוק באור, ופרט, בתופעות שונות באור המתאפיינות במראים צבעוניים מיוחדים. בחלקו הראשון של המחקר, התופעה המרכזית שחקרנו הייתה "הקשת בענן", תופעה מרהיבה שמיוחסת לה הערכה רבה בעולם המדעי, התרבותי והמיסטי. בהמשך חקרנו את הנושא הקיטוב באור. 

מטרות המחקר ושאלות המחקר:

 מטרת המחקר שלנו היא להבין תופעות אופטיות שונות כמו קשת בענן וקיטוב באור. בחלק הראשון של החקר חקרנו לעומק את תופעת הקשת בענן, בדקנו כיצד נוצרת קשת, וכיצד ניתן לשחזר קשת ביתית, כמו כן האם ניתן לשנות את צבעי הקשת ולתת לה ביטוי מתמטי. בחלק השני של החקר נכנסנו לחקר תופעת הקיטוב באור. בדקנו מדוע תופעת הקיטוב מתרחשת, מהם התנאים ההכרחיים להווצרות הצבעים, באילו חומרים התופעה מתרחשת, וכיצד המקטב יכול לגרום לשינוי הצבעים.

שאלות החקר:

1.  כיצד עוצמת האור תלויה ביחס הזוויות בין המקטבים והציר האופטי?
2.  כיצד עוצמת האור תלויה בעובי הסלוטייפ?
3. כיצד מתבצע מעבר אור בעל צבעים שונים דרך סלוטייפ?

עקרונות פיזיקליים מרכזיים

אור, שבירה, חוק סנל, התאוריה האמפירית של קוצי', תופעת הנפיצה, החזרה גמורה, מודל מעבר האור בטיפה, קיטוב באור, קיטוב לינארי, קיטוב מעגלי, חוק מאלוס, משוואות פרנל, שבירה כפולה

ניסויים מקדימים:

1. חוק סנל בלייזרים
2. חוק סנל בפריזמה משולשת
3. זוית סטיה
4. חוק מאלוס
5.  משוואות פרנל
6. משוואות פרנל באור לבן
7. פיצול אור בקלציט

ניסויים מרכזיים:

1. קשת בענן – תאודוריך
2. עוצמת האור כתלות ביחס הזוויות בין המקטבים והציר האופטי בסלוטייפ
3. שכבות סלוטייפ שונות
4. סלוטייפ בצבעים שונים

מהלך המחקר

חלק א' – קשת בענן

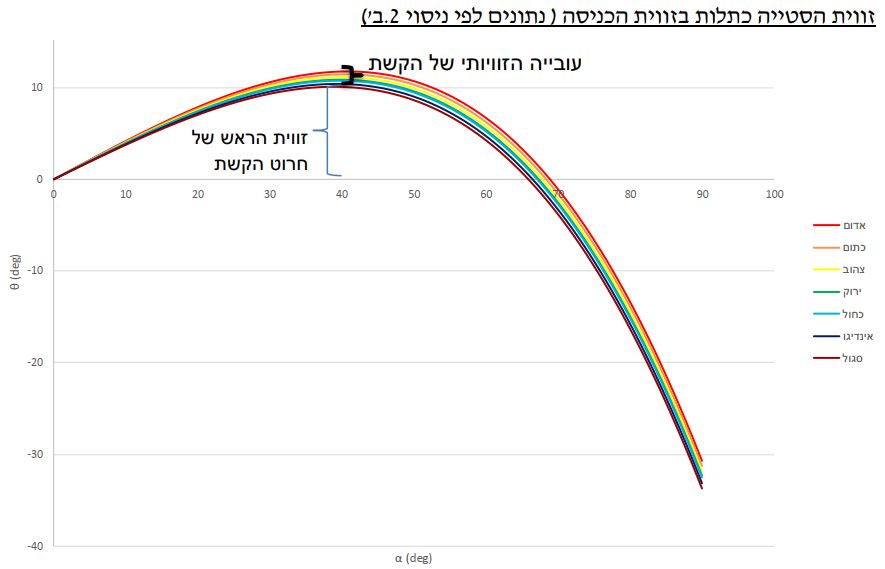
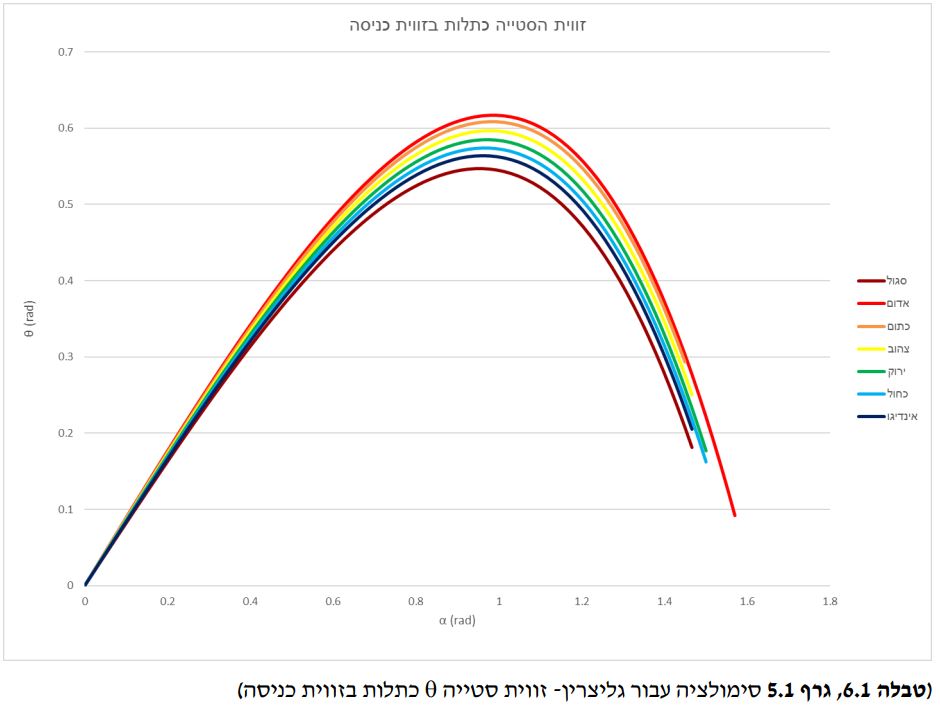
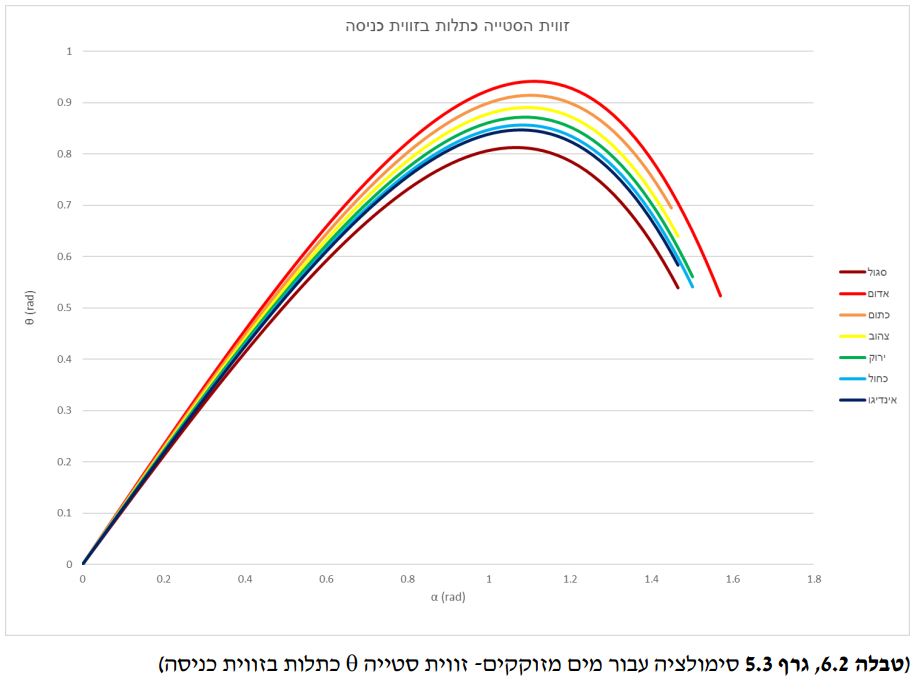
בחלק הראשון של חקירת הקשת בענן, מטרת הניסוי היתה אישוש הסימולציה שמקשרת בין מקדם השבירה לזווית הסטייה המקסימלית (שבה רואים את פס הצבע בקשת) עבור חומרים שונים ומציאת קשר בין מאפיינים שונים של הקשת (כמו עובי הקשת ורדיוס חרוט הקשת). תחילה בנינו סימולציה שבה חישבנו את זווית הסטייה של כל צבע בטיפה לפי המקדם וזוויות הכניסה של קרני האור, באמצעות שימוש בחוק סנל : ובאמצעות הנוסחה: .

בהמשך פיתחנו נוסחה של זוית הסטיה כתלות במקדם בלבד:

על מנת לאשש את התיאוריה, נחזור על ניסוי מקדים 2ועל הסימולציה שלאחריו. תחילה נבדוק את מקדמי השבירה של חומרים שונים. לאחר מכן, נבדוק האם ערכי נקודת הקיצון של פונקציית זווית הסטייה כתלות בזווית הכניסה ובמקדם תואם את ערך הנקודה עם אותו מקדם בגרף זווית הסטייה המקסימלית כתלות במקדם.

מערך הניסוי:

תוצאות ניסוי תיאודוריך:

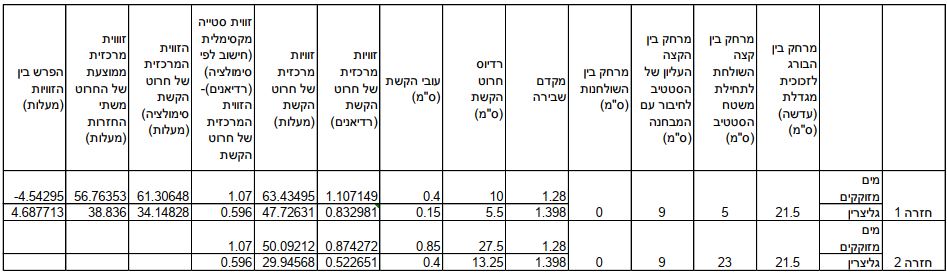
בניסוי לא יכולנו למדוד את זווית הסטייה עבור צבע, לכן מדדנו את הממוצע. עם זאת, ניתן לראות פער של 4-5מעלות בין זווית הסטייה המקסימלית שיצאה בסימולציה לזווית המרכזית של חרוט הקשת. הפרש זה הינו משמעותי במימדים של הניסוי, ואנחנו משערים שהוא קרה בגלל חוסר הדיוק של הניסוי. ניתן לראות שהזווית המרכזית של החרוט השתנתה משמעותית כששינינו את המרחקים (זה לא אמור לקרות בכלל,) וכן היה קשה לראות את ההתחלה והסוף של הקווים. הניסוי מאוד מעורפל ועל כן קשה לדייק בו. נוסף על כך, קיימות שתי שבירות בניסוי שלנו, בין האוויר לזכוכית, ובין הזכוכית למים. אנחנו משערים שגם השבירה הנוספת היא גורם להבדל בין הזווית המרכזית של החרוט בניסוי ובתיאוריה. 

חלק ב' – קיטוב באור

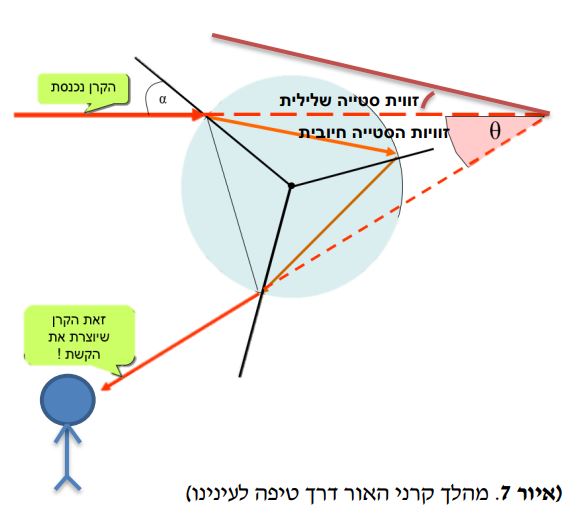
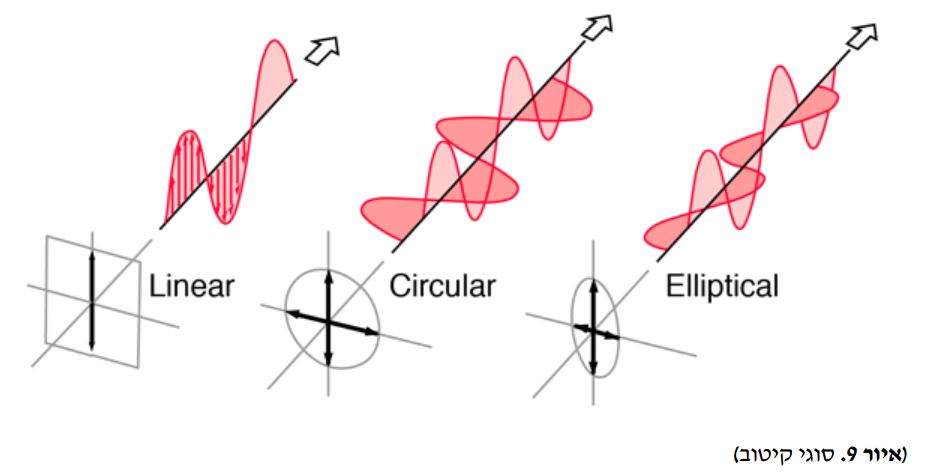
קיטוב היא תכונה של גלי האור שמכתיבה את כיוון השדה החשמלי ( שמשפיע גם על גודל). סוגי הקיטוב:

חוק מאלוס מסביר את השפעת מקטב על עוצמת האור. בפועל, חוק מאלוס מקשר בין עוצמת האור לאחר מעבר דרך מקטב אחד לעוצמת האור לאחר מעבר דרך שני מקטבים:

נוסחאות פרנל :

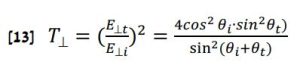
ניסוי מרכזי: עוצמת האור כתלות ביחס הזוויות בין המקטבים והציר האופטי בסלוטייפ 

סלוטייפ הוא חומר שבו מתקיימת שבירה כפולה. לכן, עוצמת האור העוברת דרך הסלוטייפ, תשתנה בהתאם ליחס הזווית בינה לבין הציר האופטי. כדי להבין תופעה זו עלינו להסביר את הפרש הפאזות המתרחש בעת המעבר. את הפרש הפאזה ניתן לחשב באמצעות הנוסחה:

לאחר הבנת הפרשי הפאזות, נוכל לבטא את הקשר בין זווית הקרן הנכנסת לעומת הציר האופטי, לבין עוצמת האור היוצאת:

מהלך הניסוי: 

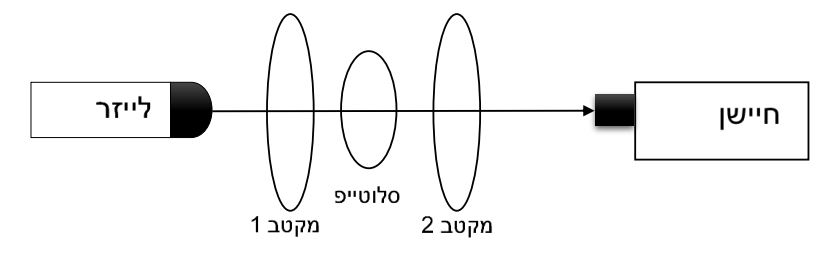
תוצאות הניסוי: 

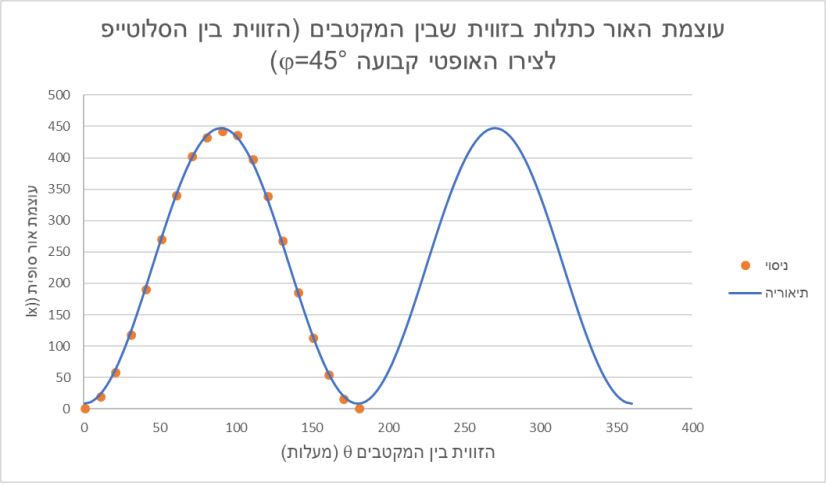
על פי התוצאות שלעיל ניתן לראות כי הצלחנו לאושש את הנוסחאות ולמצוא את הקשר בין עוצמת האור לזווית הקיטוב. מצאנו שהפרש מקדמי השבירה בסלוטייפ עבור אור אדום הוא 0.00784 (ערך התואם את טווח הערכים על פי מאמר 0.007678-0.007520 ).

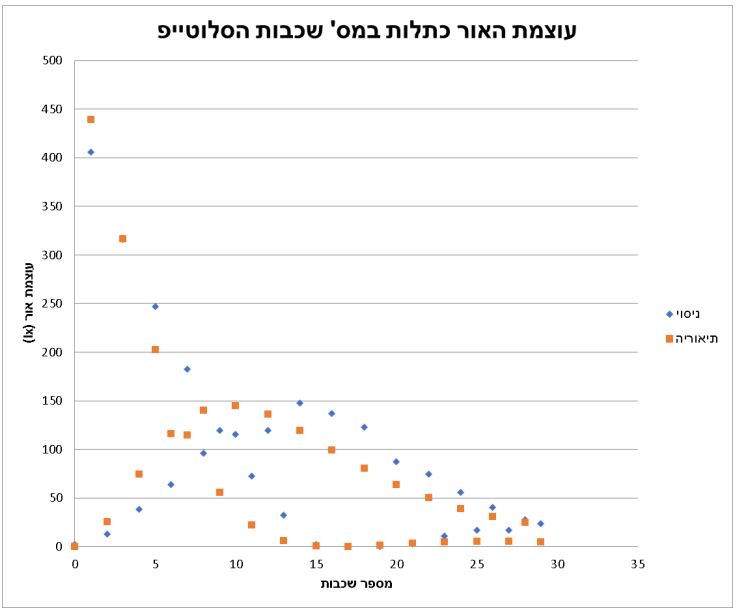
ניסוי מרכזי: עוצמת האור כתלות בעובי הסלוטייפ 

מטרת הניסוי: למצוא את הקשר בין עוצמת האור בקרן היוצאת לעובי הסלוטייפ (כדוגמה לחומר בעל שבירה כפולה). אנחנו משערים שעוצמת האור היוצאת תשתנה כתלות בעובי על פי הנוסחה :

תוצאות הניסוי: 

ניסוי מרכזי: מעבר אור בעל צבעים שונים דרך סלוטייפ 

מטרת הניסוי: אישוש התיאוריה על תלות עוצמת האור כתלות בזווית בין המקטבים ובזווית בין הציר האופטי של הסלוטייפ למקטבים. 

תוצאות הניסוי: 

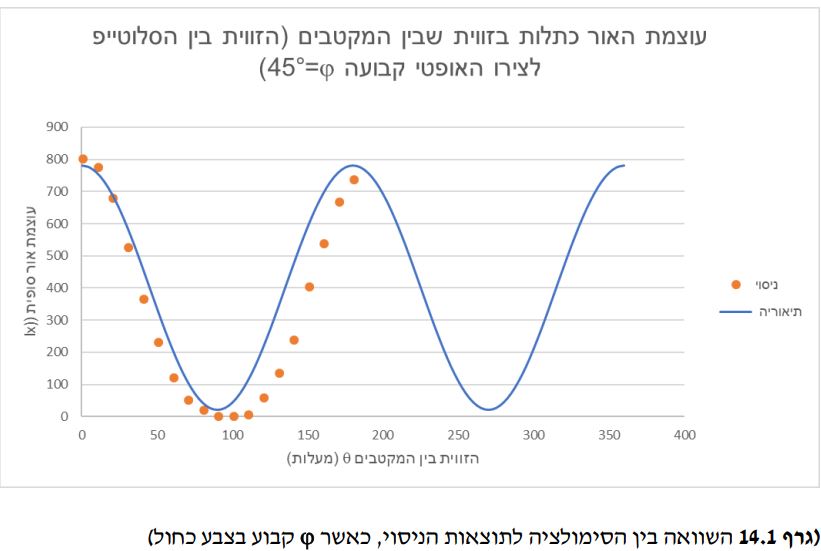
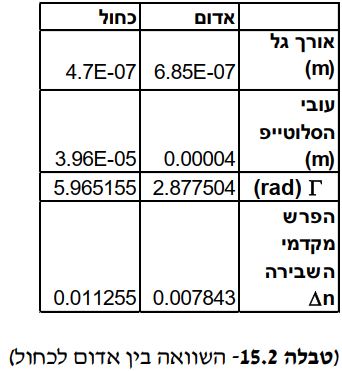
על סמך הניסוי והשוואתו לתוצאות הניסוי עבור הצבע האדום, ניתן להבין שבגלל שלכל צבע מקדם שבירה שונה, מעבר קרן האור בסלוטייפ תגרום לעוצמת האור שונה עבור כל צבע. דבר זה מאשש את השערתנו הראשונית, האומרת כי הצבע שאנו רואים לאחר מעבר דרך המקטב תלוי בעובי החומר (כאשר
החומר בעל שבירה כפולה בהכרח) ובזוויות במערכת- זאת משום שעובי החומר והזוויות יוצרים הפרשי פאזה.

ביבליוגרפיה:

1.  אריאלי ,ר.' 1993 "הקשת בענן." "הפיזיקה בחיי היום יום." המחלקה להוראת מדעים, מכון וויצמן. .75-8
2. היואיט, פ' ג.'  1997 "פיסיקה לכל," ירושלים: מכון ברנקו וייס לטיפוח החשיבה. 449-563
3. כהן, ע.' 1987 "קשת בענן- ים של טיפות ואור". ירושלים: מוסד ויצמן לפרסומים במדעי הטבע ובטכנולוגיה. 74-79 .
4. כהן, ע.' 2019 "מעשה ומחשבה בחקר מדעי". מכון מופ"ת. .
5. Akerlof, C'. (2005). “polarization”. University of Michigan. (chapter 4). physics 341 experiment
6. Beléndez, A', Fernández, E', Francés J', and Neipp, C'. (2010). “Birefringence of cellotape: Jones representation and experimental analysis”. IOP science. 551-561
7. Born, M' and Wolf, E. "Principles of Optics" and Longhurst, R' S'. (1967). "Geometrical and Physical Optics". Inside: " Dispersion". Eacharya
8. Cowen Physics (2015). "Malus' Law". Cowen Physics' YouTube channel.
9. "Khan Academy .(2005). "Polarization of light, linear and circular
10. Khanra, A', Raychaudhuri, B'. (2016). “Cello tape Birefringent Filter: Some New Demonstrations”. Optics and Photonics Journal.140-142
11. Meir, Y. “reflection and refraction”. Ben Gurion University. (unknown date). Chapter 3; 1-12.
12. "Mzough, T'. (2005). "Reflection and Refraction of Light Waves (Explanation by Huygens' Principle)
13. Professor Mittleman, D' M'. “Fresnel's Equations for Reflection and Refraction”. Brown University
14. Schwartz, M'. (2016). “lecture 14- polarization”. Harvard university.1-9